Diffusive Transport

Diffusive transport is an important phenomenon not covered in the text. Random motions of molecules (molecular diffusion) or random motions in fluids (turbulence) have a tendency to transport materials down gradients of matter or energy. If one side of a lake heated (for example by introducing waste heat from a power plant condenser), we will set up a heat gradient such that temperature changes as a function of distance from the heat source. If lake’s currents are turbulent, random motions (eddies) will form as the currents circulate in the lake. Some cool parcels of water will penetrate into the warm plume near the heat source and some warm parcels will penetrate into the cooler parts of the lake. Statistically, warm water will tend to flow away from the heat source. If we shut the plant down and stop adding heat at one point, eventually turbulent diffusion will mix the lake and distribute the heat evenly throughout the whole volume.

When more people smoked it was easier to get an intuitive idea of the dynamics of turbulent diffusion. When a smoker emits a plume of smoke, it doesn’t flow away in a straight jet. Rather, eddies form immediately, and the smoke plume begins to mix with clean air. The plume breaks down into big eddies and the big eddies develop smaller ones and so on as the plume grows in volume but shrinks in smoke concentration. As the plume slows and drifts away, eddies in air carrying it continue dilute it and eventually the smoke from any one puff is diluted into a huge volume of air.

Fluid dynamicists are much concerned with how much turbulent motion there is in a body of air or water. The equations governing turbulent motions are exceedingly complex and even though they were written down in the 19^th Century, they defy easy analysis to this day. Much of the world’s supercomputer time is devoted analyzing diffusion problems, for example in the context of numerical weather forecasting and nuclear bomb design. For more routine problems, Fick’s “Law,” a partly phenomenological model, is commonly employed. In that model, the amount of turbulent energy is represented by the coefficient of eddy diffusivity. Empirically, one can use various methods to estimate this parameter as a function of mean current or wind speeds, for example.

In some conditions, the coefficient of eddy diffusivity is nearly zero. Very slow flows or flows under conditions that inhibit the formation of eddies, such as small diameter pipes, or strongly density-stratified situations lake thermoclines, are cases where the formation of turbulent eddies is strongly suppressed. In such cases flow is said to be “laminar.”

When flows are laminar, diffusion is restricted to the random motions of molecules themselves. For example, the air spaces of soils are very small and any flows that exist tend to be laminar. Gaseous pollutants in soils gradual move through air spaces by the small-scale random, “Brownian” motions of individual molecules. Fick’s Law also describes the down-gradient motions of such pollutants well enough, albeit with a very much smaller diffusion coefficient than in the turbulent case.

Because turbulent mixing is much more rapid than molecular diffusion and because most flows of air and water are turbulent, we have a tendency to assume that most pollutants are dispersed by turbulence at respectable rates. Sometimes this assumption is violated. A friend of mine solved a strange problem that cropped up in the Geyser’s Steam Field in Lake/Sonoma Counties by recognizing an exception. Power companies drill wells into the geothermal stem field there to generate electricity. Steam wells have a fair amount of hydrogen sulfide in them, a noxious (smells like rotten eggs) and dangerous pollutant. In a small downhill community, Anderson Springs, people complained of sometimes smelling high concentrations of H₂S. Monitoring equipment also detected occasional spikes as well. Fick’s Law calculations using “reasonable” coefficients of eddy diffusivity indicated that such concentrations should never be reached so far from the offending wells. The plumes of pollutant should be very well dispersed at such a distance, several miles. The problem turned out to be that on cold, still nights, very slow-flowing down-canyon breezes with almost no turbulence “entrained” the H₂S emitted by the wells and meandered downhill with very little mixing to Anderson Springs, giving rise to pulse concentrations 100 or so times higher than a “reasonable” calculation suggested should occur.

Fick’s “Law”

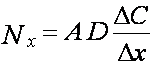
mass flux (mass * time^-1)

area of plane of diffusion (m²)

diffusion coefficient (molecular or turbulent

(m² * min^-1)

concentration difference (mg * m^-3)

distance over which concentration gradient

exists(length)

or 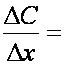concentration gradient

Example: suppose we have a 3 m long hall connecting an underground parking garage polluted with CO at 34 mg m^-3. The hall is 1 m wide and 2 m tall. At the end of the hall is an office where ventilation maintains the CO level at 10 mg m^-3. If the diffusion coefficient is 0.5 m² min^-1 what is the CO max flux toward the office?

2 m² * 0.5 m² min^-1 * 24 mg m^-3 * (3m)^-1

= 6 mg min^-1

Diffusion problem.

Suppose a restaurant owner proposes to divide his dining room into two equal sections to create a non-smoking and smoking section. Each section is 20 m long along their common wall. To partition the room the owner proposes to build a bar 15 m long along the common wall between the sections with overhead construction that restricts the opening between the sections to 1 meter high. The remaining 5 meters of common wall will be a passageway open to the ceiling (3 m high). Both rooms have ventilating systems that move 10 m³ of clean air into each room per minute, flushing out 10m³ of contaminated air. In the smoking section, the owner’s consultant estimates that the emission of smoke particulate matter by smokers filling that section on Saturday night is about 60 mg min^-1. Assume both sections are well mixed and separated by a one meter wide zone of turbulent mixing over the bar and through the passageway. During the Saturday night test by consultant the concentration of smoke in the smoking room is found to be 4 mg m^-3 and the concentration in the non-smoking room 2 mg m^-3.

A. Check to be sure the system was in equilibrium during the test.

B. Compute the coefficient of eddy diffusivity.

C. Suppose that the local standard for the concentration of smoke in non-smoking

areas is 1 mg m^-3. To what area must the owner restrict the size of

the openings between the two sections to achieve that standard?